
Статью подготовили специалисты образовательного сервиса Zaochnik.
Деление многочленов
Содержание:
В данной статье будут рассмотрены рациональные дроби, ее выделения целых частей. Дроби бывают правильными и неправильными. Когда в дроби числитель меньше знаменателя – это правильная дробь, а неправильная наоборот.
Рассмотрим примеры правильных дробей: , неправильных: .
Будем вычислять дроби, которые могут сократиться, то есть - это - это .
При выделении целой части производится процесс деления числителя на знаменатель. Тогда такая дробь может быть представлена как сумма целой и дробной части, где дробная считается отношением остатка от деления и знаменателя.
Найти остаток при делении на .
Решение
Необходимо произвести деление столбиком, тогда получим, что

Значит,
Ответ: остаток .
Произвести выделение целых частей и .
Решение
Производим деление знаменателя на числитель при помощи уголка:
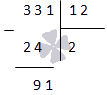
Производим деление далее и получаем, что
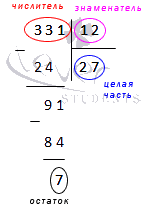
Поэтому имеем, что .
Вторая дробь является правильной, значит, целая часть равняется нулю.
Ответ: целые части и .
Рассмотрим классификацию многочленов, иначе говоря, дробно-рациональную функцию. Ее считают правильной, когда степень числителя меньше степени знаменателя, иначе ее считают неправильной.
Деление многочлена на многочлен происходит по принципу деления углом, а представление функции как сумма целой и дробной частей.
Чтобы разделить многочлен на линейный двучлен, используется схема Горнера.
Произвести деление на одночлен .
Решение
Воспользовавшись свойством деления, запишем, что
.
Зачастую такого вида преобразования выполняются при взятии интегралов.
Произвести деление многочлена на многочлен: на .
Решение
Знак деления можно записать в виде дроби вида . Теперь необходимо выделить целую часть. Производим это при помощи деления столбиком. Получаем, что
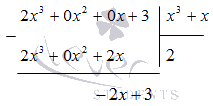
Значит, получаем, что целая часть имеет значение , тогда все выражение записывается как
Разделить и найти остаток от деления на .
Решение
Зафиксируем дробь вида .
Степень числителя больше, чем у знаменателя, значит, что у нас имеется неправильная дробь. При помощи деления столбиком выдели целую часть. Получаем, что
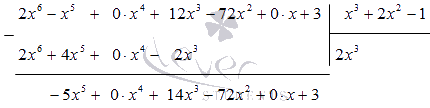
Произведем деление еще раз и получим:
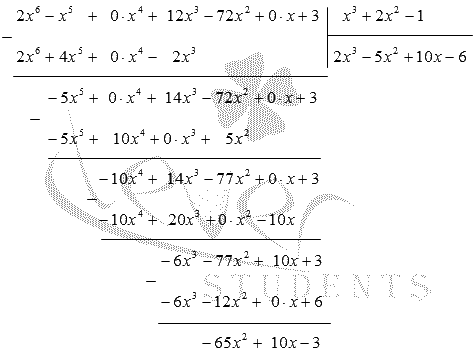
Отсюда имеем, что остаток равняется , отсюда следует:
Существуют случаи, где необходимо дополнительно выполнять преобразование дроби для того, чтобы можно было выявить остаток при делении. Это выглядит следующим образом:
Значит, что остаток при делении на дает значение . Для быстрого нахождения результата применяют формулы сокращенного умножения.
Произвести деление на .
Решение
Запишем деление в виде дроби. Получим, что . Заметим, что в числителе выражение можно сложить по формуле куба суммы. Имеем, что
Заданный многочлен делится без остатка.
Для решения используется более удобный метод решения, причем деление многочлена на многочлен считается максимально универсальным, поэтому часто используемым при выделении целой части. Итоговая запись должна содержать полученный многочлен от деления.
Навигация по статьям
