Метод Симпсона (парабол)

Содержание:

При вычислении определенного интеграла не всегда получаем точное решение. Не всегда удается представление в виде элементарной функции. Формула Ньютона-Лейбница не подходит для вычисления, поэтому необходимо использовать методы численного интегрирования. Такой метод позволяет получать данные с высокой точностью. Метод Симпсона является таковым.

Для этого необходимо дать графическое представление выведению формулы. Далее идет запись оценки абсолютной погрешности при помощи метода Симпсона. В заключении произведем сравнение трех методов: Симпсона, прямоугольников, трапеций.

Метод парабол – суть, формула, оценка, погрешности, иллюстрации

Задана функция вида $y = f (x)$ , имеющая непрерывность на интервале $[a; b]$ , необходимо произвести вычисление определенного интеграла $\int_{a}^{b} f (x) d x$

Необходимо разбить отрезок $[a; b]$ на $n$ отрезков вида $[x_{2 i - 2}; x_{2 i}], i = 1, 2, . . ., n$ с длиной $2 h = \frac{b - a}{n}$ и точками $a = x_{0} < x_{2} < x_{4} < . . . < x_{2 π - 2} < x_{2 π} = b$ . Тогда точки $x_{2 i - 1}, i = 1, 2, . . ., n$ считаются серединами отрезков $[x_{2 i - 2}; x_{2 i}], i = 1, 2, . . ., n$ . Данный случай показывает, что определение узлов производится через $x_{i} = a + i \cdot h, i = 0, 1, . . ., 2 n$ .

Суть метода парабол

Каждый интервал $[x_{2 i - 2}; x_{2 i}], i = 1, 2, . . ., n$ подынтегральной функции приближен при помощи параболы, заданной $y = a_{i} x^{2} + b_{i} x + c_{i}$ , проходящей через точки с координатами $(x_{2 i - 2}; f (x_{2 i - 2})), (x_{2 i - 1}; (x_{2 i - 1})), (x_{2 i}; f (x_{2 i}))$ . Поэтому метод и имеет такое название.

Данные действия выполняются для того, чтобы интеграл $\int_{x_{2 i - 2}}^{x_{2 i}} (a_{i} x^{2} + b_{i} x + c_{i}) d x$ взять в качестве приближенного значения $\int_{x_{2 i - 2}}^{x_{2 i}} f (x) d x$ . Можем вычислить при помощи формулы Ньютона-Лейбница. Это и есть суть метода парабол. Рассмотрим рисунок, приведенный ниже.

Суть метода парабол

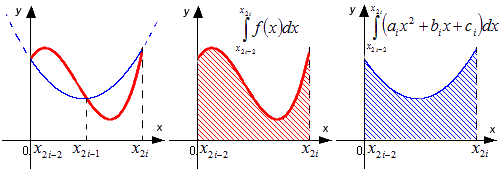
Графическая иллюстрация метода парабол (Симпсона)

При помощи красной линии изображается график функции $y = f (x)$ , синей – приближение графика $y = f (x)$ при помощи квадратичных парабол.

Суть метода парабол

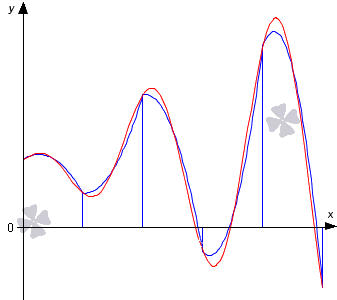
Вывод формулы метода Симпсона (парабол)

Исходя из пятого свойства определенного интеграла получаем $\int_{a}^{b} f (x) d x = \sum_{i = 1}^{n} \int_{x_{2 i - 2}}^{x_{2 i}} f (x) d x \approx \sum_{i = 1}^{n} \int_{x_{2 i - 2}}^{x_{2 i}} (a_{i} x^{2} + b_{i} x + c_{i}) d x$

Для того чтобы получить формулу методом парабол, необходимо произвести вычисление:

$\int_{x_{2 i - 2}}^{x_{2 i}} (a_{i} x^{2} + b_{i} x + c_{i}) d x$

Пусть $x_{2 i - 2} = 0$ . Рассмотрим рисунок, приведенный ниже.

Вывод формулы метода Симпсона (парабол)

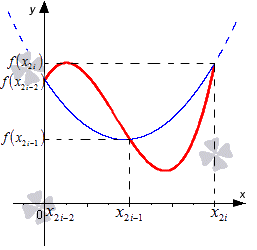
Изобразим, что через точки с координатами $(x_{2 i - 2}; f (x_{2 i - 2})), (x_{2 i - 1}; (x_{2 i - 1})), (x_{2 i}; f (x_{2 i}))$ может проходить одна квадратичная парабола вида $y = a_{i} x^{2} + b_{i} x + c_{i}$ . Иначе говоря, необходимо доказать, что коэффициенты могут определяться только единственным способом.

Имеем, что $(x_{2 i - 2}; f (x_{2 i - 2})), (x_{2 i - 1}; (x_{2 i - 1})), (x_{2 i}; f (x_{2 i}))$ являются точками параболы, тогда каждое из представленных уравнений является справедливым. Получаем, что

$\{\begin{cases} \begin{array}{l} a_{i} (x_{2 i - 2})^{2} + b_{i} \cdot x_{2 i - 2} + c_{i} = f (x_{2 i - 2}) \\ a_{i} (x_{2 i - 1})^{2} + b_{i} \cdot x_{2 i - 1} + c_{i} = f (x_{2 i - 1}) \end{array} \\ a_{i} (x_{2 i})^{2} + b_{i} \cdot x_{2 i} + c_{i} = f (x_{2 i}) \end{cases}$

Полученная система разрешается относительно $a_{i}, b_{i}, c_{i}$ , где необходимо искать определитель матрицы по Вандермонду. Получаем, что

$|\begin{matrix} (x_{2 i - 2})^{2} & x_{2 i - 2} & 1 \\ x_{2 i - 1})^{2} & x_{2 i - 1} & 1 \\ (x_{2 i})^{2} & x_{2 i} & 1 \end{matrix}|$ , причем он считается отличным от нуля и не совпадает с точками $x_{2 i - 2}, x_{2 i - 1}, x_{2 i}$ . Это признак того, что уравнение имеет только одно решение, тогда и выбранные коэффициенты $a_{i}; b_{i}; c_{i}$ могут определяться только единственным образом, тогда через точки $(x_{2 i - 2}; f (x_{2 i - 2})), (x_{2 i - 1}; (x_{2 i - 1})), (x_{2 i}; f (x_{2 i}))$ может проходить только одна парабола.

Можно переходить к нахождению интеграла $\int_{x_{2 i - 2}}^{x_{2 i}} (a_{i} x^{2} + b_{i} x + c_{i}) d x$ .

Видно, что

$f (x_{2 i - 2}) = f (0) = a_{i} \cdot 0^{2} + b_{i} \cdot 0 + c_{i} = c_{i} f (x_{2 i - 1}) = f (h) = a_{i} \cdot h^{2} + b_{i} \cdot h + c_{i} f (x_{2 i}) = f (0) = 4 a_{i} \cdot h^{2} + 2 b_{i} \cdot h + c_{i}$

Для осуществления последнего перехода необходимо использовать неравенство вида

$\int_{x_{2 i - 2}}^{x_{2 i}} (a_{i} x^{2} + b_{i} x + c_{i}) d x = \int_{0}^{2 h} (a_{i} x^{2} + b_{i} x + c_{i}) d x = = {(\frac{a_{i} x^{3}}{3} + \frac{b_{i} x^{2}}{2} + c_{i} x)}_{0}^{2 h} = \frac{8 a_{i} h^{3}}{3} + 2 b_{i} h^{2} + 2 c_{i} h = = \frac{h}{3} (8 a_{i} h^{2} + 6 b_{i} h + 6 c_{i}) = \frac{h}{3} (f (x_{2 i - 2}) + 4 f (2_{2 i - 1}) + f (x_{2 i}))$

Значит, получаем формулу, используя метод парабол:

$\int_{a}^{b} f (x) d x \approx \sum_{i = 1}^{n} \int_{x_{2 i - 2}}^{x_{2 i}} (a_{i} x^{2} + b_{i} x + c_{i}) d x = = \sum_{i = 1}^{n} \frac{h}{3} (f (x_{2 i - 2}) + 4 f (x_{2 i - 1}) + f (x_{2 i})) = = \frac{h}{3} (\begin{matrix} f (x_{0}) + 4 f (x_{1}) + f (x_{2}) + f (x_{2}) + 4 f (x_{3}) + f (x_{4}) + . . . + \\ + f (x_{2 n - 2}) + 4 f (x_{2 n - 1}) + f (x_{2 n}) \end{matrix}) = = \frac{h}{3} (f (x_{0}) + 4 \sum_{i = 1}^{n} f (x_{2 i - 1}) + 2 \sum_{i = 1}^{n - 1} f (x_{2 i}) + f (x_{2 n}))$

Определение 1

Формула метода Симпсона имеет вид $\int_{a}^{b} f (x) d x \approx \frac{h}{3} (f (x_{0}) + 4 \sum_{i = 1}^{n} f (x_{2 i - 1}) + 2 \sum_{i = 1}^{n - 1} f (x_{2 i}) + f (x_{2 n}))$ .

Формула оценки абсолютной погрешности имеет вид $|δ_{n}| \leq \frac{\underset{[a; b]}{m a x} |f^{(4)} (x)| \cdot (b - a)^{5}}{2880 n^{4}}$ .

Примеры приближенного вычисления определенных интегралов методом парабол

Метод Симпсона предполагает приближенное вычисление определенных интегралов. Чаще всего имеются два типа задач, для которых применим данный метод:

при приближенном вычислении определенного интеграла;
при нахождении приближенного значения с точностью $δ_{n}$ .

На точность вычисления влияет значение $n$ , чем выше $n$ , тем точнее промежуточные значения.

Пример 1

Вычислить определенный интеграл $\int_{0}^{5} \frac{x d x}{x^{4} + 4}$ при помощи метода Симпсона, разбивая отрезок интегрирования на $5$ частей.

Решение

По условию известно, что $a = 0; b = 5; n = 5, f (x) = \frac{x}{x^{4} + 4}$ .

Тогда запишем формулу Симпсона в виде

$\int_{a}^{b} f (x) d x \approx \frac{h}{3} (f (x_{0}) + 4 \sum_{i = 1}^{n} f (x_{2 i - 1}) + 2 \sum_{i = 1}^{n - 1} f (x_{2 i}) + f (x_{2 n}))$

Чтобы применить ее в полной мере, необходимо рассчитать шаг по формуле $h = \frac{b - a}{2 n}$ , определить точки $x_{i} = a + i \cdot h, i = 0, 1, . . ., 2 n$ и найти значения подынтегральной функции $f (x_{i}), i = 0, 1, . . ., 2 n$ .

Промежуточные вычисления необходимо округлять до $5$ знаков. Подставим значения и получим

$h = \frac{b - a}{2 n} = \frac{5 - 0}{2 \cdot 5} = 0.5$

Найдем значение функции в точках

$i = 0 : x_{i} = x_{0} = a + i \cdot h = 0 + 0 \cdot 0.5 = 0 \Rightarrow f (x_{0}) = f (0) = \frac{0}{0^{4} + 4} = 0 i = 1 : x_{i} = x_{1} = a + i \cdot h = 0 + 1 \cdot 0.5 = 0.5 \Rightarrow f (x_{1}) = f (0.5) = \frac{0.5}{0 . 5^{4} + 4} \approx 0.12308 . . . i = 10 : x_{i} = x_{10} = a + i \cdot h = 0 + 10 \cdot 0.5 = 5 \Rightarrow f (x_{10}) = f (5) = \frac{5}{5^{4} + 4} \approx 0.00795$

Наглядность и удобство оформляется в таблице, приведенной ниже

$i$	$0$	$1$	$2$	$3$	$4$	$5$
$x_{i}$	$0$	$0.5$	$1$	$1.5$	$2$	$2.5$
$f (x_{i})$	$0$	$0.12308$	$0.2$	$0.16552$	$0.1$	$0.05806$

$i$	$6$	$7$	$8$	$9$	$10$
$x_{i}$	$3$	$3.5$	$4$	$4.5$	$5$
$f (x_{i})$	$0.03529$	$0.02272$	$0.01538$	$0.01087$	$0.00795$

Необходимо подставить результаты в формулу метода парабол:

$\int_{0}^{5} \frac{x d x}{x^{4} + 4} \approx \frac{h}{3} (f (x_{0}) + 4 \sum_{i = 1}^{n} f (x_{2 i - 1}) + 2 \sum_{i = 1}^{n - 1} f (x_{2 i}) + f (x_{2 n})) = = \frac{0.5}{3} (0 + 4 \cdot (\begin{matrix} 0.12308 + 0.16552 + 0.05806 + \\ + 0.02272 + 0.01087 \end{matrix}) + 2 \cdot (\begin{matrix} 0.2 + 0.1 + \\ + 0.03529 + 0.01538 \end{matrix}) + 0.00795) \approx \approx 0.37171$

Для вычисления мы выбрали определенный интеграл, который можно вычислить по Ньютону-Лейбницу. Получим:

$\int_{0}^{5} \frac{x d x}{x^{4} + 4} = \frac{1}{2} \int_{0}^{5} \frac{d (x^{2})}{{(x^{2})}^{2} + 4} = {(\frac{1}{4} a r c t g \frac{x^{2}}{2})}_{0}^{5} = \frac{1}{4} a r c t g \frac{25}{2} \approx 0.37274$

Ответ: Результаты совпадают до сотых.

Пример 2

Вычислить неопределенный интеграл $\int_{0}^{π} (\sin \frac{3 x}{2} + \frac{1}{2}) d x$ при помощи метода Симпсона с точностью до $0, 001$ .

Решение

По условию имеем, что $а = 0, b = π, f (x) = \sin \frac{3 x}{2} + \frac{1}{2}, |δ_{n}| \leq 0.001$ . Необходимо определить значение $n$ . Для этого используется формула оценки абсолютной погрешности метода Симпсона вида $|δ_{n}| \leq \frac{\underset{[a; b]}{m a x} |f^{(4)} (x)| \cdot (b - a)^{5}}{2880 n^{4}} \leq 0.001$

Когда найдем значение $n$ , то неравенство $\frac{\underset{[a; b]}{m a x} |f^{(4)} (x)| \cdot (b - a)^{5}}{2880 n^{4}} \leq 0.001$ будет выполняться. Тогда, применив метод парабол, погрешность при вычислении не превысит $0.001$ . Последнее неравенство примет вид

$n^{4} \geq \frac{\underset{[a; b]}{m a x} |f^{(4)} (x)| \cdot (b - a)^{5}}{2.88}$

Теперь необходимо выяснить, какое наибольшее значение может принимать модуль четвертой производной.

$f' (x) = {(\sin \frac{3 x}{2} + \frac{1}{2})}^{'} = \frac{3}{2} \cos \frac{3 x}{2} \Rightarrow f'' (x) = {(\frac{3}{2} \cos \frac{3 x}{2})}^{'} = - \frac{9}{4} \sin \frac{3 x}{2} \Rightarrow f''' (x) = {(- \frac{9}{4} \sin \frac{3 x}{2})}^{'} = - \frac{27}{8} \cos \frac{3 x}{2} \Rightarrow f^{(4)} (x) = {(- \frac{27}{8} \cos \frac{3 x}{2})}^{'} = \frac{81}{16} \sin \frac{3 x}{2}$

Область определения $f^{(4)} (x) = \frac{81}{16} \sin \frac{3 x}{2}$ принадлежит интервалу $[- \frac{81}{16}; \frac{81}{16}]$ , а сам отрезок интегрирования $[0; π)$ имеет точку экстремума, из этого следует, что $\underset{[0; π]}{m a x} |f^{(4)} (x)| = \frac{81}{16}$ .

Производим подстановку:

$n^{4} \geq \frac{\underset{[a; b]}{m a x} |f^{(4)} (x)| \cdot (b - a)^{5}}{2.88} \Leftrightarrow n^{4} \geq \frac{\frac{81}{16} \cdot {(π - 0)}^{5}}{2.88} \Leftrightarrow \Leftrightarrow n^{4} > 537.9252 \Leftrightarrow |n| > 4.8159$

Получили, что $n$ – натуральное число, тогда его значение может быть равным $n = 5, 6, 7 \dots$ для начала необходимо взять значение $n = 5$ .

Действия производить аналогично предыдущему примеру. Необходимо вычислить шаг. Для этого

$h = \frac{b - a}{2 n} = \frac{π - 0}{2 \cdot 5} = \frac{π}{10}$

Найдем узлы $x_{i} = a + i \cdot h, i = 0, 1, . . ., 2 n$ , тогда значение подынтегральной функции будет иметь вид

$i = 0 : x_{i} = x_{0} = a + i \cdot h = 0 + 0 \cdot \frac{π}{10} = 0 \Rightarrow f (x_{0}) = f (0) = \sin \frac{3 \cdot 0}{2} + \frac{1}{2} = 0.5 i = 1 : x_{i} = x_{1} = a + i \cdot h = 0 + 1 \cdot \frac{π}{10} = \frac{π}{10} \Rightarrow f (x_{1}) = f (\frac{π}{10}) = \sin \frac{3 \cdot \frac{π}{10}}{2} + \frac{1}{2} \approx 0.953990 . . . i = 10 : x_{i} = x_{10} = a + i \cdot h = 0 + 10 \cdot \frac{π}{10} = π \Rightarrow f (x_{10}) = f (π) = \sin \frac{3 \cdot π}{2} + \frac{1}{2} \approx - 0.5$

Для объединения результатов запишем данные в таблицу.

$i$	$0$	$1$	$2$	$3$	$4$
$x_{i}$	$0$	$\frac{π}{10}$	$\frac{π}{5}$	$\frac{3 π}{10}$	$\frac{2 π}{5}$
$f (x_{i})$	$0.5$	$0.953990$	$1.309017$	$1.487688$	$1.451056$

$i$	$5$	$6$	$7$	$8$	$9$	$10$
$x_{i}$	$\frac{π}{2}$	$\frac{3 π}{5}$	$\frac{7 π}{10}$	$\frac{4 π}{5}$	$\frac{9 π}{10}$	$π$
$f (x_{i})$	$1.207107$	$0.809017$	$0.343566$	$- 0.087785$	$- 0.391007$	$- 0.5$

Осталось подставить значения в формулу решения методом парабол и получим

$\int_{0}^{π} (\sin \frac{3 x}{2} + \frac{1}{2}) \approx \frac{h}{3} (f (x_{0}) + 4 \sum_{i = 1}^{n} f (x_{2 i - 1}) + 2 \sum_{i = 1}^{n - 1} f (x_{2 i}) + f (x_{2 n})) = = \frac{π}{30} \cdot (0, 5 + 4 \cdot (\begin{matrix} 0.953990 + 1.487688 + 1.207107 + \\ + 0.343566 - 0.391007 \end{matrix}) + 2 \cdot (\begin{matrix} 1.309017 + 1.451056 + \\ + 0.809017 - 0.87785 \end{matrix}) - 0.5) = = 2.237650$

Метод Симпсона позволяет нам получать приближенное значение определенного интеграла $\int_{0}^{π} (\sin \frac{3 x}{2} + \frac{1}{2}) d x \approx 2.237$ с точностью до $0, 001$ .

При вычислении формулой Ньютона-Лейбница получим в результате

$\int_{0}^{π} (\sin \frac{3 x}{2} + \frac{1}{2}) d x = {(- \frac{2}{3} \cos \frac{3 x}{2} + \frac{1}{2} x)}_{0}^{π} = = - \frac{3}{2} \cos \frac{3 π}{2} + \frac{π}{2} - (- \frac{2}{3} \cos 0 + \frac{1}{2} \cdot 0) = \frac{π}{2} + \frac{2}{3} \approx 2.237463$

Ответ: $\int_{0}^{π} (\sin \frac{3 x}{2} + \frac{1}{2}) d x \approx 2.237$

Замечание

В большинстве случаях нахождение $\underset{[a; b]}{m a x} |f^{(4)} (x)|$ проблематично. Поэтому применяется альтернатива – метод парабол. Его принцип подробно разъясняется в разделе метода трапеций. Метод парабол считается предпочтительным способом для разрешения интеграла. Вычислительная погрешность влияет на результат $n$ . Чем меньше его значение, тем точнее приближенное искомое число.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта